دراسـة الـحـالـة الـعـابـرة

تحليل الدارات الكهربائية في الحالة العابرة

دراسة الحالة العابرة في دارة RC

1-    الجهد عند تفريغ المكثف

حسب قانون كيرشوف :

حيث : 

        = RC  الثابت الزمني

المعادلة الأخيرة تمثل معادلة الجهد عند تفريغ المكثف.

2-    الجهد عند شحن المكثف

 حسب قانون كيرشوف : 

مثال (1) :

في حالة الشحن للمكثف , لنفرض أن C = 10  

اكتب برنامج لرسم الجهد عبر المكثف في الحالات التاليتين :

-      R = 1 KΩ

-      R = 10 KΩ

-      R = 0.1 KΩ

الحل :

Matlab Script

c=10e-6; 

r1=1e3; 

من أجل الدارة المبينة بالشكل , التيار المار في المحارضة معدوم , في اللحظة t=0  القاطع ينتقل من النقطة a إلى النقطة b ويبقى لمدة ثانية واحدة , وبعد ذلك ينتقل القاطع من النقطة b إلى النقطة c حيث يبقى لمدة غير محدودة , بين شكل موجة التيار عبر المحارضة بالنسبة للزمن.

tau1=c*r1; 

t=0:0.002:0.05; 

v1=10*(1-exp(-t/tau1)); 

r2=10e3; 

tau2=c*r2; 

v2=10*(1-exp(-t/tau2)); 

r3=.1e3; 

tau3=c*r3; 

v3=10*(1-exp(-t/tau3)); 

plot(t,v1,'*',t,v2,'o',t,v3,'+') 

axis([0 0.06 0 12]) 

title('Charging of a capacitor with three time constants') 

xlabel('Time, s') 

ylabel('Voltage across Capacitance') 

text(0.03,5, '* for R=1 kilohms') 

text(0.03,6, 'o for R=10 kilohms') 

text(0.03,7, '+ for R=0.1 kilohms')

والشكل التالي يبين النتائج التي حصلنا عليها من البرنامج من أجل قيم مختلفة للمقاومة ..... وهو يمثل منحني شحن المكثف .

 من الشكل الناتج نستنتج أنه كلما كانت الثابتة الزمنية أكثر صغراً كلما كان زمن شحن المكثف اصغر.

مثال (2) :

في الدارة المبينة , جهد الدخل هو نبضي بإشارة مربعة لها المطال 5V وعرض النبضة 0.5s, لو كانت قيمة  C  =  10 µF , ارسم جهد الخرج  من أجل الحالات التالية : 

-         R = 1000 Ω 

-         R = 10.000 Ω

الرسم يبدأ من الصفر لينتهي زمن ثانية ونصف.

الحل :

Matlab Function

function [v,t]=rceval(r,c)

tau=r*c;

for i=1:50

    t(i)=i/100;

    v(i)=5*(1-exp(-t(i)/tau));

end

vmax=v(50);

for i=51:100

    t(i)=i/100;

    v(i)=vmax*exp(-t(i-50)/tau);

end

end

تذكرة :

يجب تسمية ملف M-file الذي يحوي تابع بنفس اسم التابع لكي يعمل .

Matlab Script

c=10.0e-6;

r1=2500;

[v1,t1] = rceval(r1,c);

r2=10000;

[v2,t2] = rceval(r2,c);

plot(t1,v1,'+r',t2,v2,'*k')

axis([0 1 0 6])

title('Response of an RC circit to pulse input')

xlabel('Time, s')

ylabel('voltage, V')

text(0.65,5.5,'+ is for 2500 ohms')

text(0.65,5.0,'* is for 10000 ohms')

والشكل الناتج (المبين بالشكل)يبين منحني الشحن والتفريغ للمكثف .

دراسة الحالة العابرة في دارة RL

الحالة الأولى

حسب قانون كيرشوف :

حيث تعطي علاقة الثابت الزمني :

إن المعادلة الأخيرة تمثل الاستجابة الطبيعية لدارة RL.

الحالة الثانية

حسب قانون كيرشوف :

الجهد عبر المقاومة :

الجهد عبر المحارضة :

 

مثال :

الحل :

-         من أجل 0 < t < 1 s  , نستخدم المعادلة :

حيث :  

-         عند اللحظة t = 1 s   :

-         من أجل t > 1 s  :

Matlab Script

tau1 = 200/100;

for k=1:20

    t(k)=k/20;

    i(k)=0.4*(1-exp(-t(k)/tau1));

end

imax=i(20);

tau2=200/200;

for k=21:120

    t(k)=k/20;

    i(k)=imax*exp(-t(k-20)/tau2);

end

plot(t,i,'o')

axis([0 6 0 0.18])

title('Current of an RL circuit')

xlabel('time , s')

ylabel('Current, A')

دراسة الحالة العابرة في دارة  RLC

من أجل الدارة المبينة بالشكل , وباستخدام قانون كيرشوف نكتب :

بمفاضلة المعادلة المبينة نحصل على المعادلة :

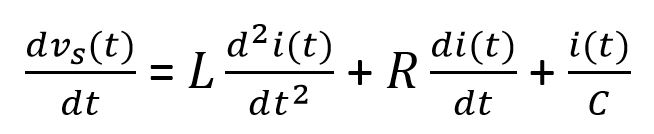
يمكن الحصول على الحل المتجانس لهذه المعادلة كالتالي :

ويمكن كتابة هذه المعادلة بالشكل :

وجذور المعادلة يمكن الحصول عليهم بسهولة وبفرض الجذور :

 فإن حل المعادلة السابقة يكون :

مثال :

للدارة السابقة لنفرض أن : 

والمطلوب إيجاد التيار .

 الحل :

بجعل Vs=0  نكتب المعادلة :  

وباستخدام الماتلاب يمكن إيجاد جذور هذه المعادلة :

Matlab Script

A=[1 40 1000];

root_A=roots(A)

      

       root_A =

                    -20.0000 +24.4949i

                    -20.0000 -24.4949i

وبعد أن حصلنا على الجذور يمكن كتابة علاقة التيار كما يلي :

وبالنتيجة :

يمكن الاستعانة بتحويلات لابلاس من أجل الحصول على التوترات والتيارات في الدارات الأكثر تعقيداً و الجدول التالي يبين تحويل لابلاس لمجموعة من التوابع.

 رباعيات الأقطاب

سأكتفي بمثال لشرح رباعيات الأقطاب.

مثال :

بفرض إن مكبر العمليات الوضح بالشكل هو مثالي فالمطلوب :

1-   أوجد العناصر الأساسية لمصفوفة الممانعات z.

2-   إذا كانت الشبكة موصلة بمنبع جهد بحيث مقاومته الداخلية 50Ω ومقاومة الحمل 1kΩ, أوجد نسبة التكبير.

3-   باستخدام الماتلاب ارسم الاستجابة الترددية للمطال.

باستخدام قانون كيرشوف نجد :

من المعادلتين الأخيرتين :

من المعادلتين 1-2 نجد :

ولإيجاد نسبة التكبير :

 ومن أجل الرسم باستخدام الماتلاب نكتب البرنامج التالي :

clc

clear

num=[2];

den=[1.05e-4 1];

w=logspace(1,5);

h=freqs(num,den,w);

f=w/(2*pi);

mag=20*log10(abs(h));

semilogx(f,mag);

title('Lowpass Filter Response')

xlabel('Frequency,Hz')

ylabel('Gain in dB')